Convert binary to hex

    Converting from binary to hex is just as easy, as it was from hex to binary. Both notations have a base that is an exact power of two (2 = 2¹ and 16 = 2⁴). To do the conversion we can just substitute the corresponding values according to the table. However, we need to pad the binary number to a complete byte, before the actual conversion.

Online binary to hex converter

Advertise on this site. I promise you will like the rates :)

How to

Converting from binary to hex is a straightforward procedure. Just remember to do the necessary padding, before making the substitution. Here is how to do the calculations:

1. Take the binary number and mark every four digits as a separate group, starting from the right-most position. Do the grouping in a way, that is convenient to you – for instance, put a little extra space between them.
2. The left most group could be incomplete ( size 1-2-3 digits, instead of four). If that is the case, add zeros to its left.
3. Substitute each group with its corresponding hex value from the table below. The result is your hex number.

Here is a table that contains the binary to hex mappings:

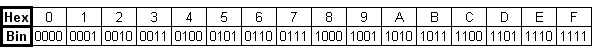
Examples

10100₂ = ?₁₆
10100₂ = 1 0100₂
1 0100₂ = 0001 0100₂
0001₂ = 1₁₆, 0100₂ = 4₁₆
10100₂ = 14₁₆

110001101010000000₂ = ?₁₆
110001101010000000 = 11 0001 1010 1000 0000
11 0001 1010 1000 0000 = 0011 0001 1010 1000 0000
0011 0001 1010 1000 0000₂ = 31A80₁₆

Making the calculations in C

    Download the complete example from here: bin-to-hex.zip
    The code is also available on GitHub.

While converting from binary to hex is very easy on paper, it could get a bit tricky to code. The key here is to do the padding and the length calculations correctly. The rest of it is just string compare and copy.

Let's start with the input. We are converting from one string type to another string. This means that we are not limited by 32-64 bit numbers. We can convert as big numbers, as we like. However, choosing a round size(like 50 or 100) for the binary string is not a good idea, because the data usually comes in complete bytes. For that reason, it is better to choose a size that is a multiple of 8, like 64, 96, 128.

1
2
3

char *hex;
char binary[97]; //96 digits + 1 terminating symbol
scanf("%96s", binary); //Don't read beyond 96 symbols to prevent overflow 

Once we read the input, it is time to begin the algorithm.

Padding with starting zeros

Note, that here we want to add zeros to a complete byte. This is, because it will be better for the output formatting of the hex value.

Padding with starting zeros is an easy task, if you apply a little smart arithmetic to calculate the necessary padding. Its length is determined only by the size of the left-most incomplete group(here we group by 8). If the group is complete, then we don't need to pad anything. If the group is of 3 digits, we need to add 5 0s before its start. To determine that size we use the formula:

     padding = 8 - length % 8;

Here length % 8 gives the number of digits in the left most group.
Once we know the padding size we allocate memory for the padded binary string. Then copy the zeros and the binary value. Finally we reset the pointer to the beginning and return the result.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

char *padBinary(char *binary, int length)
{
    int i;
    int padding = 8 - length % 8;
    int paddedBinaryLength = padding + length + 1;
    char *paddedBinary;
    if(padding == 8 || padding == 0)
        return binary;
    paddedBinary = (char *)malloc(paddedBinaryLength);
    if(paddedBinary == NULL)
        exit(1);
    for(i = 0; i < padding; ++i)
        *paddedBinary++ = '0';
    while(*binary != '\0')
        *paddedBinary++ = *binary++;
    *paddedBinary = '\0';
    paddedBinary -= paddedBinaryLength - 1;
    return paddedBinary;
}

Conversion

hexLength = strlen(paddedBinary) / 4; //We need one hex symbol for every 4 binary symbols
hexLength = hexLength + hexLength/2 + 1; //Make place for a space after every two symbols + the null terminator

Now we can convert that binary to hex. We determine the number of digits for the hexadecimal number with the formula:

I think, the comments explain it well enough.
The next step is to allocate the memory and convert every group of 4 to its hex representation. That we do with the function valueOf, according to the table above.
Finally, we reset the hex pointer and print the result.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

char *binaryToHex(char *binary, int length)
{
    int i;
    char *hex;
    char *paddedBinary = padBinary(binary, length);
    int hexLength = strlen(paddedBinary) / 4; // We need one hex symbol for every 4 binary symbols
    hexLength = hexLength + hexLength/2 + 1; // Make place for a space after every two symbols + the null terminater
    hex = (char *)malloc(hexLength);
    if(hex == NULL)
        exit(1);
    for(i = 0; i < length; i += 8)
    {
        char halfByte[5];
		// copy the 4 binary digits and decode them to one hex digit
        memcpy(halfByte, paddedBinary, 4);
        halfByte[4] = '\0';
        *hex++ = valueOf(halfByte);
        paddedBinary += 4;

        memcpy(halfByte, paddedBinary, 4);
        halfByte[4] = '\0';
        *hex++ = valueOf(halfByte);
        paddedBinary += 4;

        *hex++ = ' ';
    }
    *hex = '\0';
    hex -= hexLength - 1;
    return hex;
}

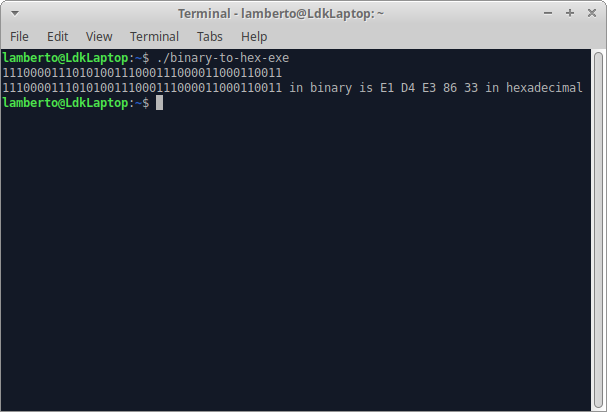
The conversion using this program looks like this:

If you liked this article, you also might want to look at:

• Hexadecimal to binary
• Binary to decimal